1601. НОД двух чисел

Найдите НОД (наибольший общий делитель) двух натуральных чисел.

Вход. Два натуральных числа a и b (a, b ≤ 2∙10⁹).

Выход. Выведите НОД чисел a и b.

Пример входа	Пример выхода
42 24	6

РЕШЕНИЕ

теория чисел - НОД

Анализ алгоритма

Наибольшим общим делителем (НОД) двух целых чисел называется наибольшее натуральное число, которое делит эти числа. Например, НОД(8, 12) = 4.

Известно, что НОД(0, x) = |x| (модуль числа x), так как |x| является наибольшим натуральным числом, которое делит 0 и x. Например, НОД(-6, 0) = 6, НОД(0, 5) = 5.

Для нахождения НОД двух чисел можно воспользоваться итеративным алгоритмом: следует вычитать меньшее число из большего. Когда одно из чисел станет равным 0, второе станет равным НОД. Например: НОД(10, 24) = НОД(10, 14) = НОД(10, 4) = НОД(6, 4) = НОД(2, 4) = НОД(2, 2) = НОД(2, 0) = 2.

Если вместо операции ‘вычитания’ использовать операцию `взятия модуля`, то вычисления пройдут значительно быстрее.

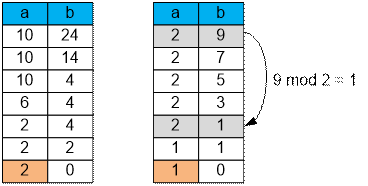
Например, для нахождения НОД(1, 10⁹) в случае использования вычитания следует совершить 10⁹ операций. При использовании операции `взятия модуля` достаточно одного действия.

НОД двух чисел можно вычислить по формуле:

НОД(a, b) = ,

или то же самое что и

НОД(a, b) =

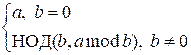
Циклическая реализация состоит в идее, приведенной в последнем рекуррентном соотношении:

пока (b > 0) :

вычисляем a = a % b;

меняем местами содержимое переменных a и b;

Реализация алгоритма

Функция gcd вычисляет НОД двух чисел.

int gcd(int a, int b)

{

if (a == 0) return b;

if (b == 0) return a;

if (a >= b) return gcd(a % b, b);

return gcd(a, b % a);

}

Основная часть программы. Читаем входные данные.

scanf("%d %d",&a,&b);

Вычисляем и выводим НОД двух чисел.

d = gcd(a,b);

printf("%d\n",d);

Реализация алгоритма – упрощенная рекурсия

Функция gcd вычисляет НОД двух чисел.

int gcd(int a, int b)

{

return (!b) ? a : gcd(b,a % b);

}

Основная часть программы. Читаем входные данные.

scanf("%d %d",&a,&b);

Вычисляем и выводим НОД двух чисел.

d = gcd(a,b);

printf("%d\n",d);

Реализация алгоритма – цикл

Функция gcd вычисляет НОД двух чисел.

int gcd(int a, int b)

{

while (b > 0)

{

a = a % b;

int temp = a; a = b; b = temp;

}

return a;

}

Основная часть программы. Читаем входные данные.

scanf("%d %d",&a,&b);

Вычисляем и выводим НОД двух чисел.

d = gcd(a,b);

printf("%d\n",d);

Java реализация

import java.util.*;

public class Main

{

static int gcd(int a, int b)

{

if (a == 0) return b;

if (b == 0) return a;

if (a >= b) return gcd(a % b, b);

return gcd(a, b % a);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int a = con.nextInt();

int b = con.nextInt();

int res = gcd(a, b);

System.out.println(res);

con.close();

}

}

Python реализация – рекурсия

Функция gcd вычисляет НОД двух чисел.

def gcd(a, b):

if a == 0: return b

if b == 0: return a

if a > b: return gcd(a % b, b)

return gcd(a, b % a)

Основная часть программы. Читаем входные данные.

a, b = map(int, input().split())

Вычисляем и выводим НОД двух чисел.

print(gcd(a, b))

Python реализация – gcd

Для вычисления НОД двух чисел воспользуемся функцией gcd, встроенной в языке Питон.

 
import math
 

Читаем входные данные.

 
a, b = map(int, input().split())
 

Вычисляем и выводим НОД двух чисел.

 
print(math.gcd(a, b))